 Klasse 5
Klasse 5
 Klasse 6
Klasse 6
 Klasse 7
Klasse 7
 Klasse 8
Klasse 8
 Klasse 9
Klasse 9
 Klasse 10
Klasse 10
 Fit für die Oberstufe
Fit für die Oberstufe
nach Aufgabentypen suchen
Aufgabentypen anhand von Beispielen durchstöbern
Browserfenster aktualisieren (F5), um neue Beispiele bei den Aufgabentypen zu sehen
Extremwertaufgaben (Anwend.)
Beispiel:
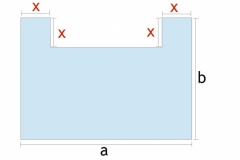
Aus einer rechteckigen Fläche, die a= cm breit und b=cm hoch ist soll oben ein Rechteck entfernt werden, so dass links oben und rechts oben noch zwei gleiche Quadrate stehen bleiben (siehe Skizze). Welche Seitenlänge müssen diese Quadrate haben, damit der Flächeninhalt der übrig gebliebenen Fläche (in der Skizze hellblau) minimal wird?
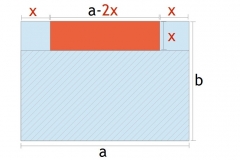
1. Weg
Man erweitert die ersten beiden Summanden ( ) zu einem 'binomischen Formel'-Term. Dazu teilt man die durch 2x und quadriert diese Ergebnis -4 zu 16. Diese 16 fügt man dann an dritter Stelle in die Summe ein. So erhält man einen Term der Form x² ± 2xb + b², den man mit der binomischen Formel als (x ± b)² schreiben kann. Damit der Funktionsterm aber nicht verändert wird muss man die 16, die man an 3. Stelle eingefügt hat, danach auch wieder abziehen.
=
=
=
=
Jetzt kann man den Scheitel leicht ablesen: S(4|-16).
2. Weg
Von können wir aber über Ausklammern und den Satz vom Nullprodukt sehr leicht die Nullstellen bestimmen.
| = | |||
| = |
Ein Produkt ist genau dann =0, wenn mindestens einer der beiden Faktoren =0 ist.
1. Fall:
| x1 | = |
2. Fall:
| = | | | ||
| x2 | = |
Aus Symmetriegründen muss der Scheitel genau in der Mitte zwischen den Nullstellen liegen, also S(4|y).
y = = = -16
also: S(4|-16).
Für x=4 bekommen wir also mit -16 einen extremalen Wert von
