Mathebattle EduRandomtasks

Raumdiagonale

Beispiel:

Ein Quader hat die Kantenlängen a = 9 mm, b = 5 mm und c = 3 mm.
Berechne die Länge der Raumdiagonale.

Die Bodendiagonale d1 ist die Hypotenuse eines rechtwinklingen Dreiecks mit den Katheten a = 9 mm und b = 5 mm, folglich gilt nach dem Satz des Pythagoras:

d1² = a² +b² = (9 mm)² + (5 mm)² = 81 mm² + 25 mm² = 106 mm²

d1 = $\sqrt{106}$ mm ≈ 10.296 mm

Die gesuchte Raumdiagonale ist d ist die Hypotenuse des rechtwinklingen Dreiecks mit den Katheten d1 und c, folglich gilt nach dem Satz des Pythagoras:

d² = d1² + c² = ( $\sqrt{106}$ mm)² + (3 mm)² = 106 mm² + 9 mm² = 115 mm²

Da d1² = a² +b² gilt, kann man die Raumdiagonale auch schneller mit der Formel
d² = a² + b² + c² = 81 mm² + 25 mm² + 9 mm² = 115 mm²
berechnen.

d = $\sqrt{115}$ mm ≈ 10.724 mm

Dreiecke im Quader

Beispiel:

Ein Quader hat die Kantenlängen a = 3 m, b = 3 m und c = 7 m.
Berechne den Umfang U und den Flächeninhalt A des abgebildeten (grünen) Dreiecks.

Lösung einblenden

Die Frontwanddiagonale d1 ist die Hypotenuse eines rechtwinklingen Dreiecks mit den Katheten a= 3 m und c = 7 m, folglich gilt nach dem Satz des Pythagoras:

d1² = a² + c² = (3 m)² + (7 m)² = 9 m² + 49 m² = 58 m²

d1 = $\sqrt{58}$ m ≈ 7.616 m

Die Raumdiagonale ist d ist die Hypotenuse des rechtwinklingen Dreiecks mit den Katheten d1 und b, folglich gilt nach dem Satz des Pythagoras:

d² = d1² + b² = ( $\sqrt{58}$ m)² + (3 m)² = 58 m² + 9 m² = 67 m²

d = $\sqrt{67}$ m ≈ 8.185 m

Für den Umfang U gilt somit:
U = d1 + d + b ≈ 7.62 m + 8.19 m + 3 m ≈ 18.8 m

Für den Flächeninhalt A gilt dann wegen des rechten Winkels zwischen d1 und 3:
A = $\frac{1}{2}$ d1 ⋅b ≈ $\frac{1}{2}$ ⋅7.62 m⋅ 3 m ≈ 11.42 m²

Kanten bei einer Pyramide nur vorwärts

Beispiel:

Eine gerade Pyramide hat eine rechteckige Grundfläche mit den folgenden Längen: a = 4 mm, b = 4 mm, h = 5 mm.
Berechne h_b und s.

Lösung einblenden

Wir suchen nach rechtwinkligen Dreiecken in der Pyramide um den Satz des Pythagoras anwenden zu können:

Wir erkennen in der Skizze ein rechtwinkliges Dreieck mit der Hypotenuse h_b, einer Kathete h und der anderen Kathete $\frac{1}{2}$ a (gestrichelt dargestellt auf der Bodenfläche). Also gilt:

h_b² = h² + ( $\frac{1}{2}$ a)²

Da ja h und a gegeben sind, können wir einfach einsetzen:

h_b² = 5² + 2 ² = 25 + 4 = 29

Also gilt h_b = $\sqrt{29}$ mm ≈ 5,4 mm

Wir erkennen in der Skizze ein rechtwinkliges Dreieck mit der Hypotenuse s, einer Kathete h_b und der anderen Kathete $\frac{1}{2}$ b (rechts nach hinten auf der Bodenfläche dargestellt). Also gilt:

s² = h_b² + ( $\frac{1}{2}$ b)²

Da ja h_b und b gegeben sind, können wir einfach einsetzen:

s = 5,39² + 2² = 29,05 + 4 = 33

Also gilt s = $\sqrt{33.05}$ mm ≈ 5,8 mm

Kanten bei einer Pyramide

Beispiel:

Eine gerade Pyramide hat eine rechteckige Grundfläche mit den folgenden Längen: b = 4 m, h = 7 m, s = 8.1 m.
Berechne a und h_b.

Lösung einblenden

Wir suchen nach rechtwinkligen Dreiecken in der Pyramide um den Satz des Pythagoras anwenden zu können:

Wir erkennen in der Skizze ein rechtwinkliges Dreieck mit der Hypotenuse s, einer Kathete h_b und der anderen Kathete $\frac{1}{2}$ b (rechts nach hinten auf der Bodenfläche dargestellt). Also gilt:

s² = h_b² + ( $\frac{1}{2}$ b)²

Weil wir h_b suchen, stellen wir nach h_b um:

s² - ( $\frac{1}{2}$ b)² = h_b ²

h_b² = 8,1² - 2² = 65,61 - 4 = 61,61

Also gilt h_b = $\sqrt{61.61}$ m ≈ 7,8 m

Wir erkennen in der Skizze ein rechtwinkliges Dreieck mit der Hypotenuse h_b, einer Kathete h und der anderen Kathete $\frac{1}{2}$ a (gestrichelt dargestellt auf der Bodenfläche). Also gilt:

h_b² = h² + ( $\frac{1}{2}$ a)²

Weil wir a suchen, stellen wir nach a um:

( $\frac{1}{2}$ a)² = h_b² - h²

( $\frac{1}{2}$ a)² = 7,85² - 7² = 61,61 - 49 = 12,61

Also gilt $\frac{1}{2}$ a = $\sqrt{12.61}$ m ≈ 3,6 m

Somit gilt: a ≈ 7,1 m

Anwendungen Pythagoras

Beispiel:

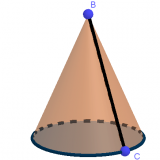
Ein Kegel ist 35 cm hoch. Sein Grundkreis hat einen Durchmesser von 40 cm. Wie lang ist die Strecke von einem Punkt auf dem Grundkreis zur Spitze?

Lösung einblenden

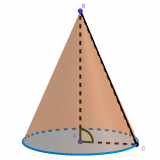
Es gilt:

20² + 35² =h²

400 +1225 = h²

1625 = h² | $\sqrt[]{\cdot}$

40.31 ≈ h

Somit gilt für die gesuchte Hypotenuse:
h ≈ 40.31cm

Pyramide (Oberflächenberechnung)

Beispiel:

Eine gerade Pyramide hat eine quadratische Grundfläche mit den folgenden Größen:
Pyramidenhöhe h = 5 m und Höhe der Seitenfläche ha = 5,83 m.
Berechne die Grundflächenlänge a und die Oberfläche O.

Lösung einblenden

Bestimmung der Grundflächenlänge a

Wir erkennen in der Skizze ein rechtwinkliges Dreieck mit der Hypotenuse h_a, einer Kathete h und der anderen Kathete $\frac{1}{2}$ a (gestrichelt dargestellt auf der Bodenfläche). Also gilt:

h_a² = h² + ( $\frac{1}{2}$ a)²

Weil wir a suchen, stellen wir nach a um:

( $\frac{1}{2}$ a)² = h_a² - h²

( $\frac{1}{2}$ a)² = 5,83² - 5² = 34 - 25 = 9

Also gilt $\frac{1}{2}$ a = $\sqrt{9}$ m ≈ 3 m

Somit gilt: a ≈ 6 m

Bestimmung der Oberfläche O

Um die Oberfläche dieser Pyramide zu bestimmen, müssen wir einfach den Mantel und die Grundfläche addieren:

Die Mantelfläche M besteht aus den 4 gleich großen Flächeninhalten der Seitenflächen dieser Pyramide. Diese soll nun berechnet werden:

Die Grundflächelänge a ist ja mit a = 6 m bereits bekannt.

Den Flächeninhalt einer Seitenfläche können wir ja einfach mit der Formel A_S= $\frac{1}{2}$ a⋅h_a berechen:

A_S = $\frac{1}{2}$ ⋅6 m⋅5,83 m ≈ 17,49 m²

Für die Mantelfläche müssen wir nun diese 4 Flächeninhalte noch zusammenzählen:

M = 4⋅17,49 m² = 69,97 m²

Um die Grundfläche dieser Pyramide zu bestimmen, müssen wir einfach die Grundflächenlänge a zum Quadrat nehmen:

Die Grundflächelänge a ist ja mit a = 6 m bereits bekannt.

somit gilt: G = a² = (6 m)² = 36 m²

somit gilt: O = M + G = 69,97 m² + 36 m² = 105,97 m²

Pyramide (Volumenberechnung)

Beispiel:

Eine gerade Pyramide hat eine quadratische Grundfläche mit den folgenden Größen:
Pyramidenhöhe h = 7 m und Grundflächenlänge a = 6 m.
Berechne die Grundfläche G und die Kantenlänge s.

Lösung einblenden

Bestimmung der Grundfläche G

Um die Grundfläche dieser Pyramide zu bestimmen, müssen wir einfach die Grundflächenlänge a zum Quadrat nehmen:

Die Grundflächelänge a ist ja mit a = 6 m bereits bekannt.

somit gilt: G = a² = (6 m)² = 36 m²

Bestimmung der Kantenlänge s

Um s zu berechnen, müssen wir zuerst die Seitenhöhe h_a berechnen:

Die Grundflächenlänge a ist ja mit a = 6 m bereits bekannt.

Die Pyramindenhöhe h ist ja mit h = 7 m bereits bekannt.

Wir erkennen in der Skizze ein rechtwinkliges Dreieck mit der Hypotenuse h_a, einer Kathete h und der anderen Kathete $\frac{1}{2}$ a (gestrichelt dargestellt auf der Bodenfläche). Also gilt:

h_a² = h² + ( $\frac{1}{2}$ a)²

Da ja h und a gegeben sind, können wir einfach einsetzen:

h_a² = 7² + 3 ² = 49 + 9 = 58

Also gilt h_a = $\sqrt{58}$ m ≈ 7,62 m

Die Grundflächelänge a ist ja mit a = 6 m bereits bekannt.

Wir erkennen in der Skizze ein rechtwinkliges Dreieck mit der Hypotenuse s, einer Kathete h_a und der anderen Kathete $\frac{1}{2}$ a (rechts nach hinten auf der Bodenfläche dargestellt). Also gilt:

s² = h_a² + ( $\frac{1}{2}$ a)²

Da ja h_a und a gegeben sind, können wir einfach einsetzen:

s = 7,62² + 3² = 58,06 + 9 = 67

Also gilt s = $\sqrt{67.06}$ m ≈ 8,19 m

Aufgabentypen anhand von Beispielen durchstöbern

Raumdiagonale

Dreiecke im Quader

Kanten bei einer Pyramide nur vorwärts

Kanten bei einer Pyramide

Anwendungen Pythagoras

Pyramide (Oberflächenberechnung)

Bestimmung der Grundflächenlänge a

Bestimmung der Oberfläche O

Pyramide (Volumenberechnung)

Bestimmung der Grundfläche G

Bestimmung der Kantenlänge s